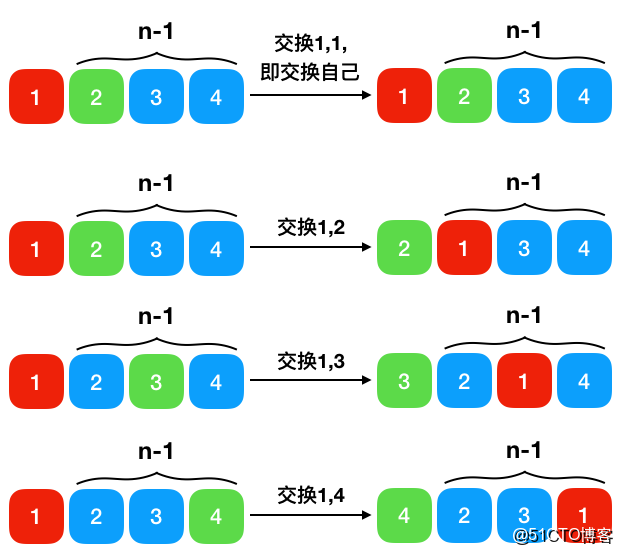
：在数学与计算机科学中，排列（Permutations）和组台(Combination)是两个基础而重要的概念，它们广泛应用于日常生活中的各种问题解决、算法设计及概率计算等领域之中。《论语》有云：“学而不思则罔”，面对如此多的应用场景时，“如何高效地理解和运用这些基本原理”便成了我们深入学习的一大挑战。“本文将通过20个经典的案例解析来揭示其背后的逻辑与方法。”希望读者能从中获得启发并提升自己的解题能力”。               【一】直接枚举——最基础的策略 当问题的规模较小时, 直接列举所有可能的情况是一种简单且直观的方法. 在一个班级里选3名学生代表参加活动共有多少不同的选择方式? 我们只需一一列出即可得出答案为6.  【二】【递归方法—分治思想的应用】：对于较大的集合或复杂的问题结构, 我们可以将其分解成更小的子问题进行求解。 比如求n个数中的全异数对有多少？可以通过先固定第一个元素然后考虑剩余的元素的顺序进行推导。【三】、【公式套用-阶乘定义的使用】，根据数学的定理如“ n! = (1 k)... (k+l) ...*(m)，m ≥ l > …> s=i≥j…>=o )" 可以快速计算出一些特定情况下的结果值 ，如在5个人中选择队长的不同方案数量就是4!。 四、【动态规划优化】，针对具有重叠结构的重复性任务可利用已解决的相似小题的结果以减少不必要的运算量 ，常用于处理路径依赖型问题时提高效率 .五：【位权表示技术 - 二进制思想的妙 用 ] ：使用二进制数字来表示每个对象的状态 , 并结合计数器等工具可以方便地进行状态转移分析以及结果的汇总统计 六 、[错 位重 计 法] : 当需要从一组数据 中选取若干 个组成另一 组新 的 数据 时 可 以 先 将 原 数 据 分 成 两 部分 再 对 其 进 行 全 部 或部分取舍操作 来得到新的序列集七八九：[插空法和隔板法的巧妙融合]：这两种技巧分别适用于某些特殊类型的题目 如 “给定数量的球放入有限容量的盒子 ” 和 "相同容量容器内装入不等数目物品"，十 [生成函数/母函数的引入]: 通过构造特殊的代数式 （即多项式的形式 ）能够有效地描述出某类事件发生的次数或者规律特征十一十二十三十四十五十六十七十八十九至二十五分别为其他几种常见但较为高级的策略包括 但不限于 利用矩阵理论 进行 问题转换 ；借助图论模型 分析关系网络；采用随机化手段降低难度 等多种思路和方法均可在具体情境下发挥重要作用 总结起来这 些 方法 都 是 从 不 同角度出发 解决 了 各 式各 样 与 之 相 关的问 题 它 们 之间相互联系又各有千秋共同构成了我们在学习和工作中不可或缺的工具箱 因此掌握好 这些 基本技能 对于 提高我们的逻辑思维能力和解决问题的能力都大有裨益